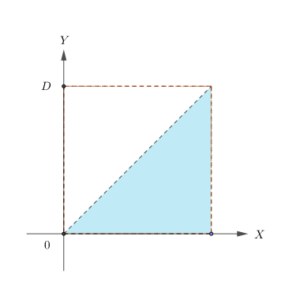
La función de densidad de probabilidad (fdp) conjunta de una variable aleatoria bidimensional \((X,Y)\) es uniforme en la región sombreada en el gráfico, donde \(D\) es una constante.
a) Escriba la expresión correspondiente de la fdp conjunta de \(X\) e \(Y.\) Compruebe que es fdp.
b) Calcule \(P(X \lt D/2, Y \lt D/4)\).
c) Calcule las fdp marginales, de \(X\) y de \(Y.\) Compruebe en ambos casos que realmente son fdp.