En el artículo Aritmética del reloj se introdujo el tema, en éste se profundiza en la definición de congruencia. Allí se vió que sumando o restando a una hora \(h\)cualquier múltiplo del módulo siempre obteníamos como resultado la misma hora \(h\). En la siguiente tabla vemos que cada vez que nos movamos cinco unidades a derecha o izquierda se repetirá el resto de la división por \(5\) \(\def\bmag#1{\bf\color{magenta}{#1}}\def\equivmod#1{\mathbin {\mathop \equiv_{#1}}}\def\otimesmod#1{\mathbin{\mathop{\otimes}_{#1}}}\def\oplusmod#1{\mathbin{\mathop{\oplus}_{#1}}} \def\clasemod#1#2{\left [\, #2 \, \right ]_{#1}}\def\invmod#1#2{{\clasemod{#1} {#2}}^{-1}}\def\divent#1#2#3#4{#1 = #2 \times #3 + #4}\) $$\begin{array}{r|r|c|r|r|r|r|c|r|r|r} \cdots & +4 & \bbox[cyan,5px] {5 \times 3} & +1 & +2 & +3 & +4 & \bbox[cyan,5px] {5 \times 4} & +1 & +2 & \cdots \\ \hline \cdots & \bmag {14} & \bbox[yellow,5px]{\bmag {15}} & \bmag {16} & \bmag {17} & \bmag {18} & \bmag {19} & \bbox[yellow,5px]{\bmag {20}} & \bmag {21} & \bmag {22} & \cdots \\ \hline \cdots & 4 & \bbox[cyan,5px]{0} & 1 & 2 & 3 & 4 & \bbox[cyan,5px]{0} & 1 & 2 & \cdots \end{array}$$
En general \(a = 5 \times k + r, \quad \text{con } 0 \le r \lt 5\), y añadiendo o quitando múltiplos de \(5\) el resto \(r\) no cambiará.
Con este módulo de \(5\) unidades podemos construir los sectores de una ruleta donde distribuir los números enteros: vamos desplegando los números en una espiral alrededor del centro, los positivos crecen desde el \(0\) hacia el exterior y los negativos se distribuyen hacia el centro de la ruleta.

Ya ves que cada sector aloja aquellos números que dan el mismo resto al dividirlos entre el módulo \(5\). ¿En qué sector encontraríamos al número \(-17\)? Dividamos entre 5 y el resto nos dará la respuesta: $$-17 = 5 \times (-4) + 3 \tag{1}\label{eq1}$$ Está señalado el sector que contiene al \(3\) y a todos los números obtenidos sumándole múltiplos del módulo. Si continuamos colocando los negativos \(-6, -7, -8, \dotsc,\) llegaremos a colocar \(-17\) en este mismo sector como habíamos deducido en la igualdad \(\eqref{eq1}\). Este sector lo nombramos \(\clasemod{5} 3\) (el menor entero no negativo que está en él), aunque podría identificarse por otro entero cualquiera de ese sector: \(\clasemod{5} 3\), \(\clasemod{5} {-2}\), \(\clasemod{5} {13}\), pues cada entero aparece en un único sector. El sector \(\clasemod{5} 0\) contiene los múltiplos de \(5\); todos ellos dan resto \(0\) al dividirlos entre \(5\). De la misma forma, el sector \(\clasemod{5} 1\) contiene todos los números que dan resto \(1\) al dividirlos entre \(5\). Cada entero se encuentra en uno de los cinco conjuntos siguientes: $$\begin{alignat}{4} \clasemod{5} 0 &= \{ \dots, -10, -5, &0&, 5, 10, 15,\dots \} &\quad \dot 5 + 0 \\ \clasemod{5} 1 &= \{ \dots, -\phantom{1}9, -4, &1&, 6, 11, 16,\dots \} &\quad \dot 5 + 1\\ \clasemod{5} 2 &= \{ \dots, -\phantom{1}8, -3, &2&, 7, 12, 17,\dots \} &\quad \dot 5 + 2 \\ \clasemod{5} 3 &= \{ \dots, -\phantom{1}7, -2, &3&, 8, 13, 18,\dots \} &\quad \dot 5 + 3 \\ \clasemod{5} 4 &= \{ \dots, -\phantom{1}6, -1, &4&, 9, 14, 19,\dots \} &\quad \dot 5 + 4 \end{alignat}$$
Veamos qué sucede si cambiamos al módulo \(24\). La ruleta de \(24\) sectores muestra una nueva clasificación de los números enteros. Como antes, el sector en rojo \(\clasemod{24} 0\) contiene los múltiplos del módulo. El sector \(\clasemod{24} 3\) contiene ahora la colección de enteros \(\dotsc, -21, 3, 27, 51, \dotsc \) que son los números \(\dot {24} + 3\). Tendríamos clasificados los enteros en \(24\) conjuntos (sectores de la ruleta) \(\clasemod{24} 0, \clasemod{24} 1, \dots, \clasemod{24} {23}\)

Congruencia módulo un número natural
Va siendo hora de dar nombre a las cosas. Dos números que se encuentren en el mismo sector tienen común el resto cuando se dividen entre el módulo, entonces diremos que son congruentes.
Dado un número entero \(a\) se dice que otro número \(b\) es congruente con \(a\) módulo \(n\), y se escribe \(b \equivmod{n} a\), si ambos números dan el mismo resto \(r\) al dividirlos entre \(n\). Esto equivale a decir que su diferencia es múltiplo de \(n\), \(b -a = \dot n\). El conjunto que tiene por elementos a todos los enteros congruentes con \(a\) módulo \(n\) se denota por \(\clasemod{n} a\) y se puede describir como $$\clasemod{n} a = \left \{ a+ n \times k \mid k \in \mathbb Z \right \}\tag{2}\label{eq2}$$ se llama clase de congruencia de \(a\) módulo \(n\). $$a \equivmod{n} b \iff \clasemod{n} a = \clasemod{n} b.\tag{3}\label{eq3}$$
Como la división entera de \(a\) entre \(n\) nos permite expresarlo como un múltiplo de \(n\) más un resto
$$a = n \cdot k + r \quad \text{ con } 0 \le r \lt n$$ entonces \(\clasemod{n} a = \clasemod{n} r\). Por tanto, solo hay \(n\) clases de congruencia módulo \(n\) que son $$\clasemod{n} 0, \clasemod{n} 1, \dotsc, \clasemod{n} {n -1}\tag{4}\label{eq4}$$
En nuestra analogía, el conjunto de clases es la ruleta y las clases de congruencia, sus sectores. Cuando no hay lugar a confusión, suele identificarse el conjunto de clases con el conjunto de números \(\mathbb Z_n\) (así se presentan las tablas de las operaciones más adelante)$$\mathbb Z_n = \left \{ 0, 1,\dots,n -1 \right \}$$
La notación clásica para la congruencia módulo \(n\) se ha sustituido por una forma abreviada más económica de presentación $$\begin{matrix} \text{cl$\rm\acute a$sica} && \text{abreviada} \\ a \equiv b \pmod{n} && a \equivmod{n} {b} \quad o \quad \displaystyle{ a \equivmod{n} {b} } \end{matrix}$$
Con el lenguaje de congruencias expresamos algunas propiedades que las hacen muy semejantes a las igualdades de números enteros: $$\eqalign {a \equivmod{n} b \mathbin{\small \wedge} a’ \equivmod{n} b’ &\iff &(a+a’) \equivmod{n} (b+b’) \\ a \equivmod{n} b \mathbin{\small \wedge} a’ \equivmod{n} b’ &\iff &(a \times a’) \equivmod{n} (b \times b’) \\ \text{tambi$\rm \acute e$n,} \\ m \in \mathbb N \mathbin{\small \wedge} a \equivmod{n} b &\iff &a^m \equivmod{n} b^m \\ c \in \mathbb Z \mathbin{\small \wedge} a \equivmod{n} b &\iff &(a + c) \equivmod{n} (b + c) \\ c \in \mathbb Z \mathbin{\small \wedge} a \equivmod{n}{b} &\Longrightarrow &(a \times c) \equivmod{n} (b \times c)}$$
La cancelación del factor \(c\) en la última congruencia solo es posible cuando \(\text{mcd}(c, n) = 1\), es decir si son coprimos.
La suma y el producto módulo n
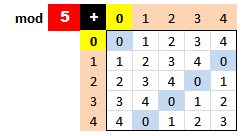
¿Qué pasaría si sumamos un entero de \(\clasemod{5} 1\) con otro entero de \(\clasemod{5} 3\)? ¿En qué clase estaría el resultado? El primero es un múltiplo de \(5\) más una unidad, el segundo, un múltiplo de \(5\) más tres unidades, su suma es \((\dot 5 + 1) + (\dot 5 + 3) = (\dot 5 + 4)\). Así, podemos escribir $$\clasemod{5} 1 \oplusmod{} \clasemod{5} 3 = \clasemod{5} {1+3} = \clasemod{5} 4 \\ \clasemod{5} {126} \oplusmod{} \clasemod{5} {628} = \clasemod{5} 1 \oplusmod{} \clasemod{5} 3 = \clasemod{5} 4 \\ \clasemod{5} {126} \oplusmod{} \clasemod{5} {628} = \clasemod{5} {754} = \clasemod{5} 4 $$ en general $$\clasemod{5} a \oplusmod{} \clasemod{5} b = \clasemod{5} {a+b}$$
La clase \( \clasemod{5} 0 \) actúa como neutro para la suma. \(\clasemod{5} 4 \oplusmod{} \clasemod{5} 0\) significa \((\dot 5 + 4) + (\dot 5 + 0) = (\dot 5 + 4)\), por tanto \(\clasemod{5} 4 \oplusmod{} \clasemod{5} 0 = \clasemod{5} 4 \)$$\clasemod{5} a \oplusmod{} \clasemod{5} 0 = \clasemod{5} a$$
Hay clases que suman la clase \(\clasemod{5} 0\). Por ejemplo \(\clasemod{5} 2 + \clasemod{5} 3 = \clasemod{5} {2 + 3} = \clasemod{5} 0\) y, en este sentido la clase \(\clasemod{5} 3\) es opuesta de la clase \(\clasemod{5} 2\) y viceversa \(\clasemod{5} 3 = -\clasemod{5} 2\). Toda clase tiene opuesta ya que si \(0 \le r \lt 5\), entonces $$\clasemod{5} r \oplusmod{} \clasemod{5} {5-r} = \clasemod{5} 0$$
Probemos a «sumar» \(\clasemod{5} 3\) con \(\clasemod{5} 4\). Sería \((\dot 5 + 3) + (\dot 5 + 4) = (\dot 5 + 7) = (\dot 5 + 2)\), es decir $$\clasemod{5} 3 \oplusmod{} \clasemod{5} 4 = \clasemod{5} {3+4} = \clasemod{5} 7 = \clasemod{5} 2$$
La tabla que rige esta operación \(\oplusmod{}\) en \(\mathbb Z_5\) es la siguiente[ 1 ]:
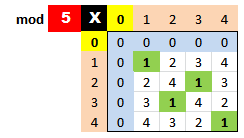
¿Si multiplicamos cualquier entero de \(\clasemod{5} 1\) con cualquier entero de \(\clasemod{5} 3\) qué obtenemos? Trabajando con múltiplos: \((\dot 5 + 1) \times (\dot 5 + 3) = (\dot 5 +1 \times 3) = (\dot 5 +3)\) y se cumple $$\clasemod{5} 3 \otimesmod{} \clasemod{5} 1 = \clasemod{5} {3 \times 1} = \clasemod{5} 3$$ y esto ocurre siempre con \(\clasemod{5} 1\) $$\clasemod{5} a \otimesmod{} \clasemod{5} 1 = \clasemod{5} a$$
Hay algunos productos de más interés como $$\clasemod{5} 2 \otimesmod{} \clasemod{5} 3 = \clasemod{5} {6} = \clasemod{5} 1 \\ \clasemod{5} 4 \otimesmod{} \clasemod{5} 4 = \clasemod{5} {16} = \clasemod{5} 1$$ que nos dicen que toda clase distinta de \(\clasemod{5} 0\) tiene inverso para el producto módulo \(5\) $$\invmod{5} 2 = \clasemod{5} 3 \\ \invmod{5} 3 = \clasemod{5} 2 \\ \invmod{5} 4 = \clasemod{5} 4$$ Esto no ocurre con otros módulos como veremos más adelante. La tabla que rige el producto \(\otimesmod{}\) en \(\mathbb Z_5\) es
Si \(a, b\) son dos enteros cualesquiera podemos operar con sus clases de congruencia módulo \(n\) de la siguiente forma: $$\eqalign {\clasemod{n} a \oplusmod{n} \clasemod{n} b &= \clasemod{n} {a+b} \\ \clasemod{n} a \otimesmod{n} \clasemod{n} b &= \clasemod{n} {a \times b}}$$
Analizamos la suma y el producto cuando el módulo es primo
Las propiedades de la suma \(\oplusmod{n}\) no varían por el hecho de ser \(n\) primo o no serlo. Cualquiera que sea \(n\) (primo o no), la suma tiene elemento neutro \(\clasemod{n} 0\) y todas las clases tienen opuesto. El producto \(\otimesmod{n}\) siempre tiene unidad \(\clasemod{n} 1\), pero la existencia de inversos se ve afectada por el carácter primo del módulo.
Si el módulo \(n\) es primo, todas las clases son invertibles. Como puedes ver en los productos en \({\mathbb Z}_{11}\) y en \({\mathbb Z}_{13}\), los unos dentro de la tabla son resultado de multiplicar dos clases invertibles: $$\eqalign {\clasemod{11} 5 \otimesmod{} \clasemod{11} 9 &= \clasemod{11} {45} = \clasemod{11} 1 \\ \clasemod{13} {10} \otimesmod{} \clasemod{13} 4 &= \clasemod{13} {40} = \clasemod{13} 1}$$

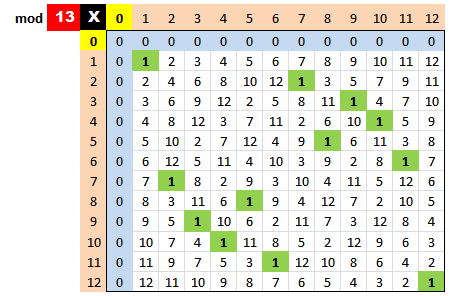
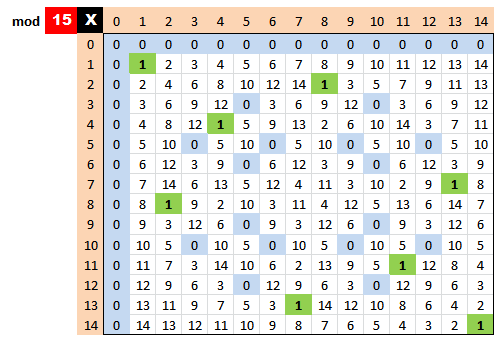
Cuando \(n\) es compuesto aparecen ceros en el interior de la tabla, resultado de multiplicar dos clases distintas de \(\clasemod{n} 0\). Por este hecho, estas clases se dice que son «divisores de cero». $$\eqalign{\clasemod{12} {9} \otimesmod{} \clasemod{12} 8 &= \clasemod{12} 0 \\ \clasemod{15} {12} \otimesmod{} \clasemod{15} 5 &= \clasemod{15} 0 }$$
En consecuencia, decir que \(\clasemod{n} a\) es invertible equivale a decir que son coprimos \(a\) y el módulo \(n\). $$\clasemod{15} 7 \otimesmod{} \clasemod{15} {13} = \clasemod{15} {91} = \clasemod{15} 1$$

[ 1 ] Las tablas de las operaciones se han realizado en una hoja de cálculo MS Excel® utilizando la función RESIDUO(número;módulo) que calcula el resto de la división entera de número entre módulo para cualquier valor entero de número. Desafortunadamente la función COCIENTE(número;módulo) solo da el cociente de la división entera cuando número es positivo. Para obtener el cociente en todos los casos debes utilizar ENTERO(número/módulo).
